PT137.S2.Q23 > Analytics

SECTION 1 · rc

PASSAGE 1

Question 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7

PASSAGE 2

Question 8 Question 9 Question 10 Question 11 Question 12 Question 13 Question 14

PASSAGE 3

Question 15 Question 16 Question 17 Question 18 Question 19

PASSAGE 4

Question 20 Question 21 Question 22 Question 23 Question 24 Question 25 Question 26 Question 27

SECTION 2 · lr

Question 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7 Question 8 Question 9 Question 10 Question 11 Question 12 Question 13 Question 14 Question 15 Question 16 Question 17 Question 18 Question 19 Question 20 Question 21 Question 22 Question 23 Question 24 Question 25

SECTION 3 · lr

SECTION 4 · lr

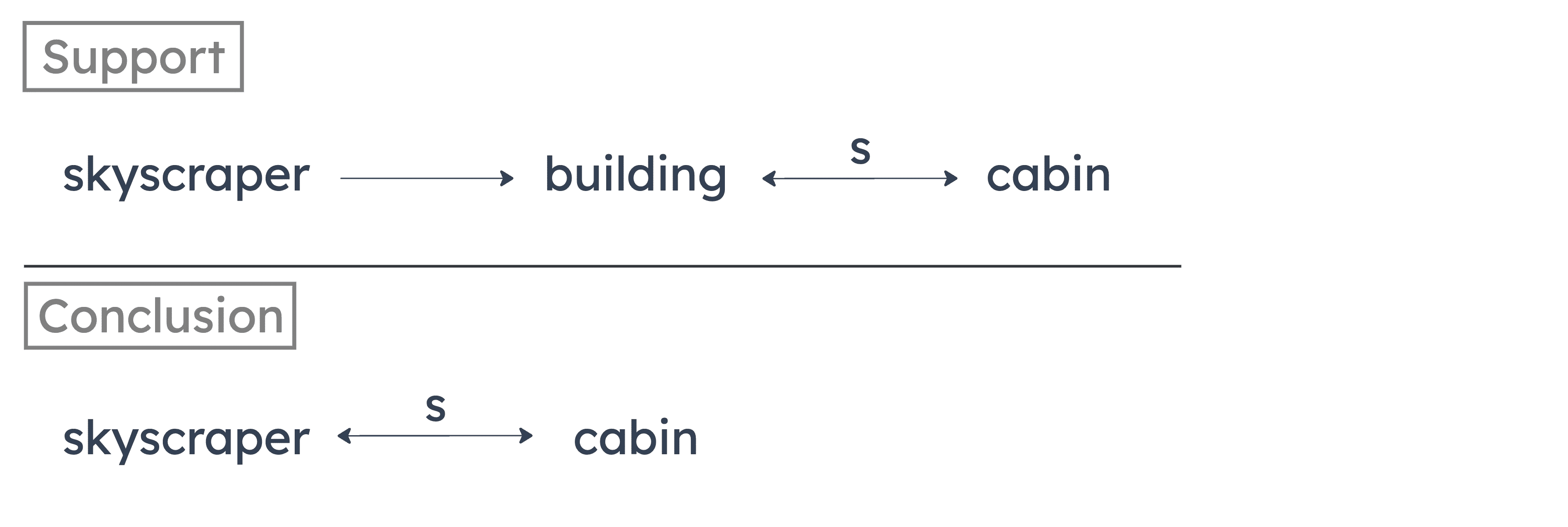
The argument presents two premises: a conditional statement and a “some” statement. It then chains the two statements together to draw another “some” statement as a conclusion.

This argument features bad conditional reasoning. If the “some” statement was in the first part of the diagram and followed by the conditional statement, then we could validly infer a “some” relationship between the first and last variables. But in this argument, a conditional statement is instead followed by a “some” statement, which is invalid. It’s like concluding that some middle school students play for the NBA, since all middle school students live in America, and some Americans play for the NBA.

Wrong flaw. (A) incorrectly chains up two “some” statements to draw its conclusion. The stimulus, however, chains up a conditional statement with a “some” statement, so (A) doesn’t match.

(B) presents two premises: a conditional statement and a “some” statement. It then incorrectly chains them up to draw a “some” conclusion. The stimulus also chains up a conditional statement and a “some” statement to draw an incorrect “some” conclusion, so (B) matches.

Wrong flaw. (C) sets up a conditional relationship: If something is a table or a chair, then it’s furniture. It then concludes that there is some relationship present between the two sufficient conditions, which is unsupported. The stimulus, however, chains up a conditional statement with a “some” statement to reach its conclusion, so (C) doesn’t match.

Wrong flaw. (D) sets up a conditional statement (if supermarket, then sell food) and a some statement (some foods are asparagus). It then invalidly concludes that all supermarkets sell asparagus. The stimulus, however, chains up a conditional statement with a “some” statement to reach a “some” conclusion, so (D) doesn’t match.

Wrong flaw. (E) incorrectly chains up two “some” statements to draw its conclusion. The stimulus, however, chains up a conditional statement with a “some” statement, so (E) doesn’t match.

Question

65% of people who answer get this correct

This is a difficult question.

CURVE

Score of students with a 50% chance of getting this right

25% 149

158

75% 167

Question Stem Tags

Parallel flawed method of reasoning

Stimulus Tags

Conditional reasoning

Quantifier

Popularity Avg. score

10%

162

65%

166

11%

160

158

You don't have any history with this question.. yet!

PrepTest 137 - Section 2 - Question 23

Difficulty

Analysis

Answer Popularity

Question history

Confirm action