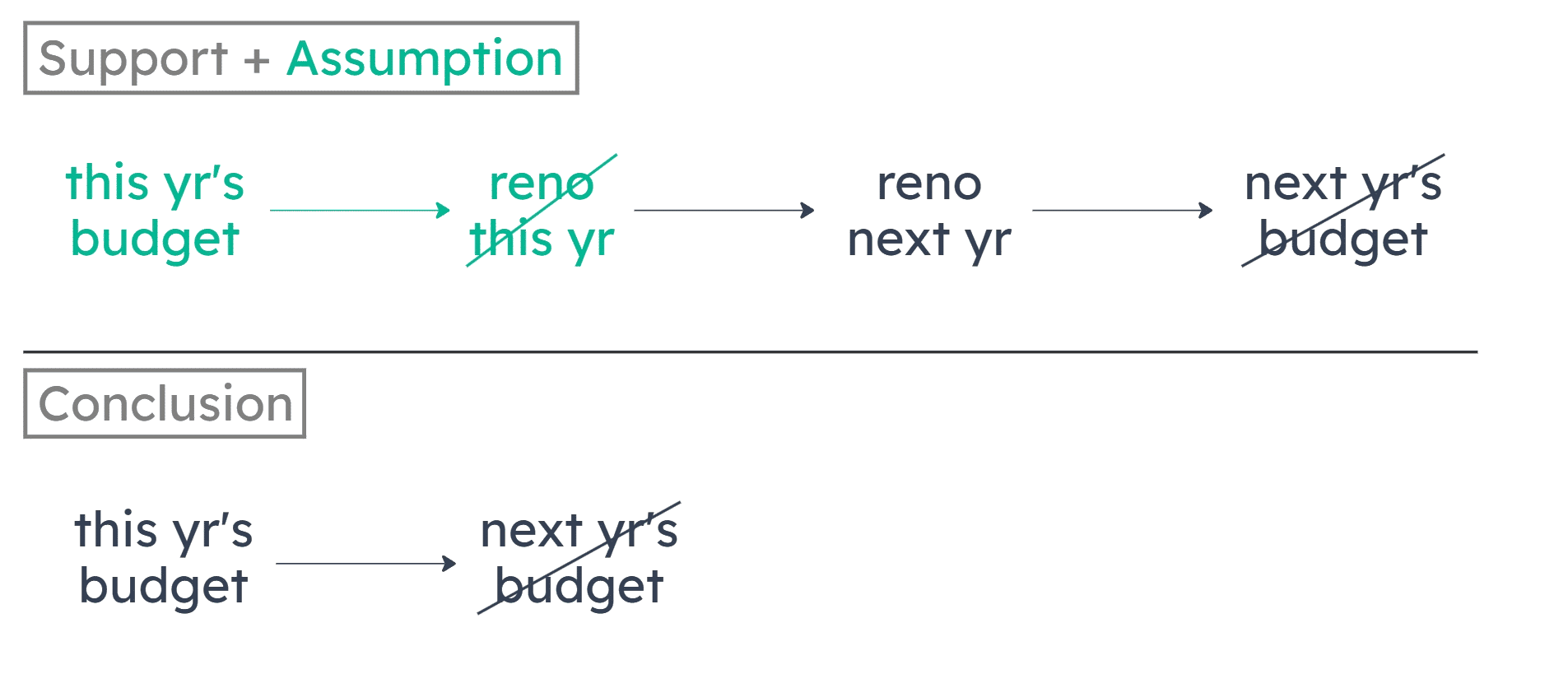
If the natural history museum stays within this year's budget, it will be unable to stay within next year's budget, for renovating next year will make the museum's expenditures exceed next year's very tight budget. █████ ████ ███ ██████ ████ ████ ██ ████████ ████ ████ ██ ██ ████ ███ ██ ██ ████ █████ ███████ ████ ████ ████████ ███████████ ██ █████████████ ████████
If the museum stays within this year’s budget, it won’t stay within next year’s budget. To support this conclusion, we’re given two conditional premises:
(1) If the museum doesn’t renovate this year, it must renovate next year.
(2) If the museum renovates next year, it won’t stay within next year’s budget.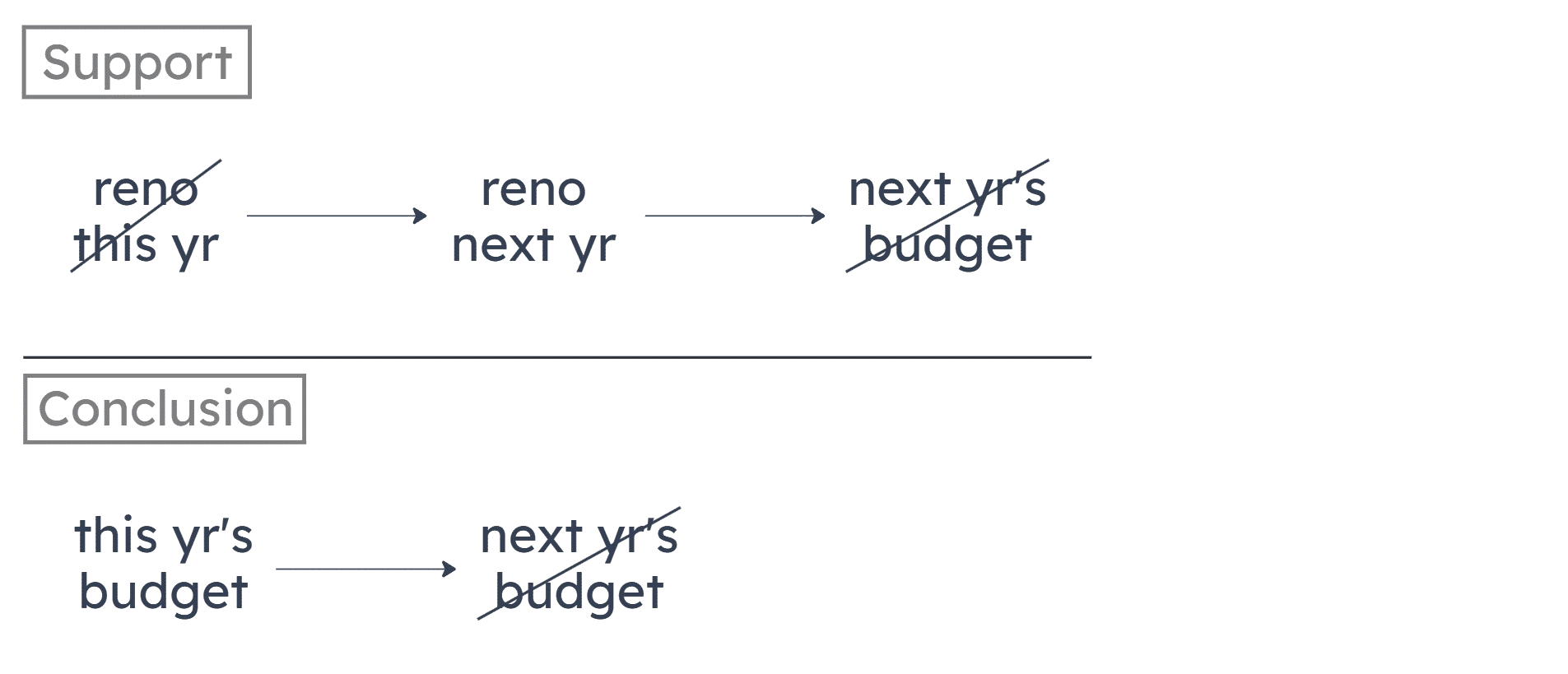
The conclusion is a conditional claim involving this year’s budget, but this year’s budget doesn’t appear anywhere in the premises. Rather, the premises are all about how renovations will affect next year’s budget. So the correct answer must connect this year’s budget to those premises.
Specifically, we can reach the author’s conclusion if we assume that to stay within this year’s budget, the museum must not renovate this year. (Contrapositive: If the museum renovates this year, it must not stay within this year’s budget.)
The argument's conclusion can be ████████ ████████ ██ █████ ███ ██ ███ █████████ ██ ████████
The museum will ████ ██████ ████ ██████ ███████
This year's budget ██ ████ ████ ████ ██████ ███████
The museum will ███ ████████ ████ █████
The museum will ██████ ████ ██████ ██████ ██ ██ █████████ ████ █████
The museum will ████ ██████ ████ ██████ ██████ ██ ██ ████ ███ ████████ ████ █████